|
The exponential function, f(x) = e x displays a unique property when looking at its derivative. This exercise help to determine this property.
Procedure:
1. Graph the natural exponential function, f(x) = e x. 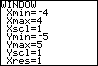
Use a window corresponding to values in the image.
In MODE change to get 4 places of decimals only. |