|
Show all work for each question. For graphs make an accurate sketch based on the TI-83's graphics screen display using the given window values. Graph each quadratic function, and then complete all the required information. The general quadratic function is f(x) =ax 2 + bx + c
The axis of symmetry is the vertical line through the vertex and the parabola is symmetric around that line. The coordinates of the vertex are ( - b/2a, f( - b/2a)).
1. f(x) = x 2 + 8x + 11
|
|
|
|
Vertex coordinates: |
|
|
Axis of Symmetry: |
|
|
x intercepts: |
|
|
y intercept: |
|
|
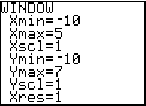
2. g(x) = - x 2 - 4x + 1
|
|
|
|
Vertex coordinates: |
|
|
Axis of Symmetry: |
|
|
x intercepts: |
|
|
y intercept |
|
|
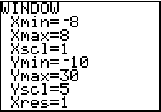
3. h(x) = 25 - x 2
|
|
|
|
Vertex coordinates: |
|
|
Axis of Symmetry: |
|
|
x intercepts: |
|
|
y intercept: |
|
|
4. f(x) = x 2 - 3x + 0.25
|

|
|
|
Vertex coordinates: |
|
|
Axis of Symmetry: |
|
|
x intercepts: |
|
|
y intercept: |
|
|
5. g(x) = - 2 x 2 - 2 x + 25 For this question graph use window values that will give a fair representation of the graph. Write your window values in the box. (Replace the zeros)
|

|

|
|
Vertex coordinates: |
|
|
Axis of Symmetry: |
|
|
x intercepts: |
|
|
y intercept: |
|
|
6. The quarterback of a football team attempts to throw a pass to his receiver who will be 90 feet away at the point where he must catch the ball. The path of the ball will be given by the quadratic function, f(x) = - 0.0139 x 2 + 1.3333 x + 7. The receiver can jump a maximum of 10 feet to catch the ball.
a) Sketch the complete graph of the quarterback's pass.
b) Write the values you used for the window . (Replace the zeros)
c) Find the maximum height of the pass and the horizontal distance from the quarterback at that point.
d) How far from the quarterback does the ball hit the ground?
e) Will the receiver catch the ball? Why?
|

|

|
|
a) |
|
|
b) |
|
|
c) |
|
|
d) |
|
|
e) |
|
|
|